« Toutes les sage-femmes vous le diront, à la pleine Lune, c’est la folie à la maternité ». Et pourtant, non. Les données ne montrent absolument rien de tel.
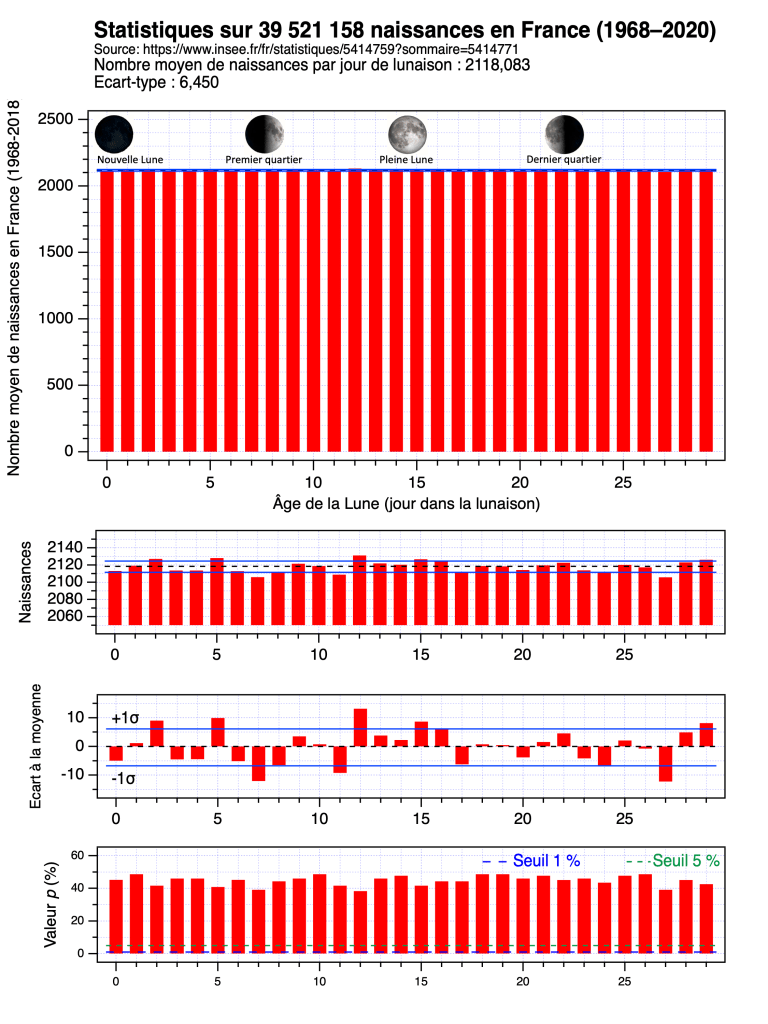
Voici les données françaises de l’INSEE de toutes les naissances de 1968 à 2020, classées par jour de lunaison. On n’observe absolument aucune variation statistiquement significative.
Le panneau du bas donne la « valeur p » qui est la probabilité, ici pour chaque jour de lunaison, de trouver un écart à la moyenne (de 2118 naissances par jour) au moins aussi « extrême » que celui observé. On est très au-delà des seuils usuels de 5 % et 1 %.
La Lune n’influence donc pas les naissances. Si tel avait été le cas, il aurait fallu en trouver le mécanisme exact. Mais cela est inutile, vu l’absence de phénomène. Comme le disait Fontenelle dans son texte « La dent d’or », « Assurons nous bien du fait, avant de nous inquiéter de la cause » !
Les données de l’INSEE :
https://www.insee.fr/fr/statistiques/5414759?sommaire=5414771
Une algorithme de calcul de la phase lunaire en fonction de la date:
https://ui.adsabs.harvard.edu/abs/1964LAstr..78..354P/abstract
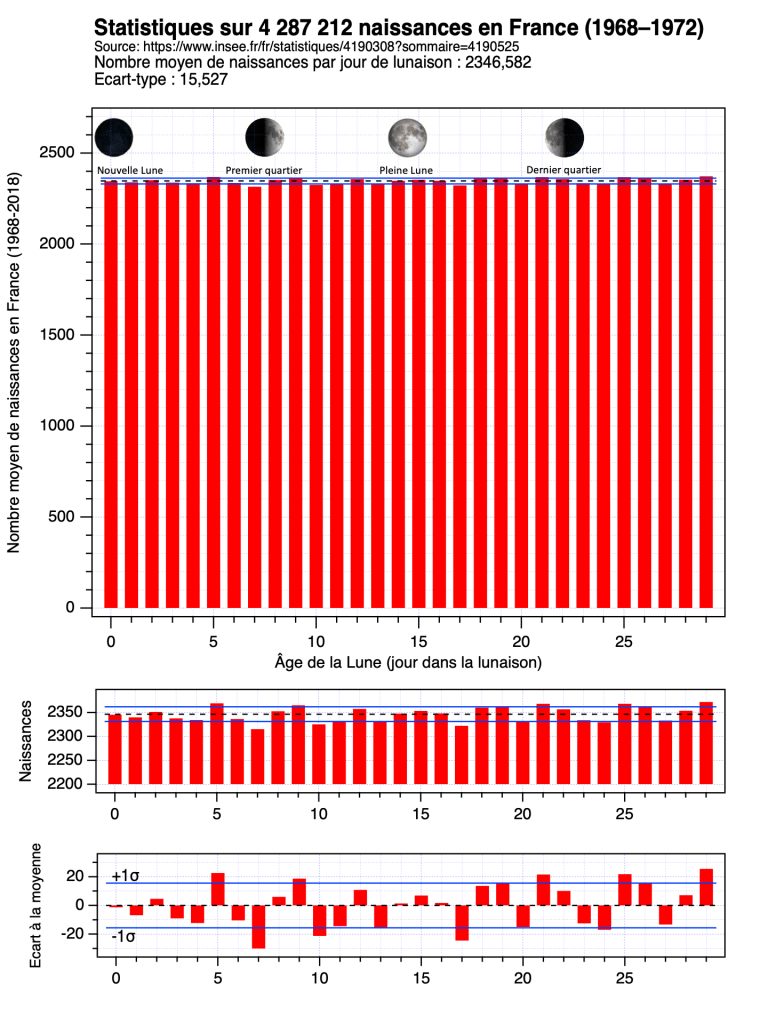
Une remarque souvent faite est que beaucoup d’accouchements sont, de nos jours, déclenchés. Il y aurait en particulier moins d’accouchements les week-ends est jours fériés. Mais cela ne change rien au présent problème car cette supposée augmentation des naissances à la pleine Lune est bel et bien évoquée actuellement, malgré les accouchements déclenchés, or on voit qu’il n’en est rien. De plus, la même statistique sur les 5 premières années disponibles à l’INSEE (1968-1972), alors que les accouchements étaient plus largement « naturels », ne montre rien de différent.
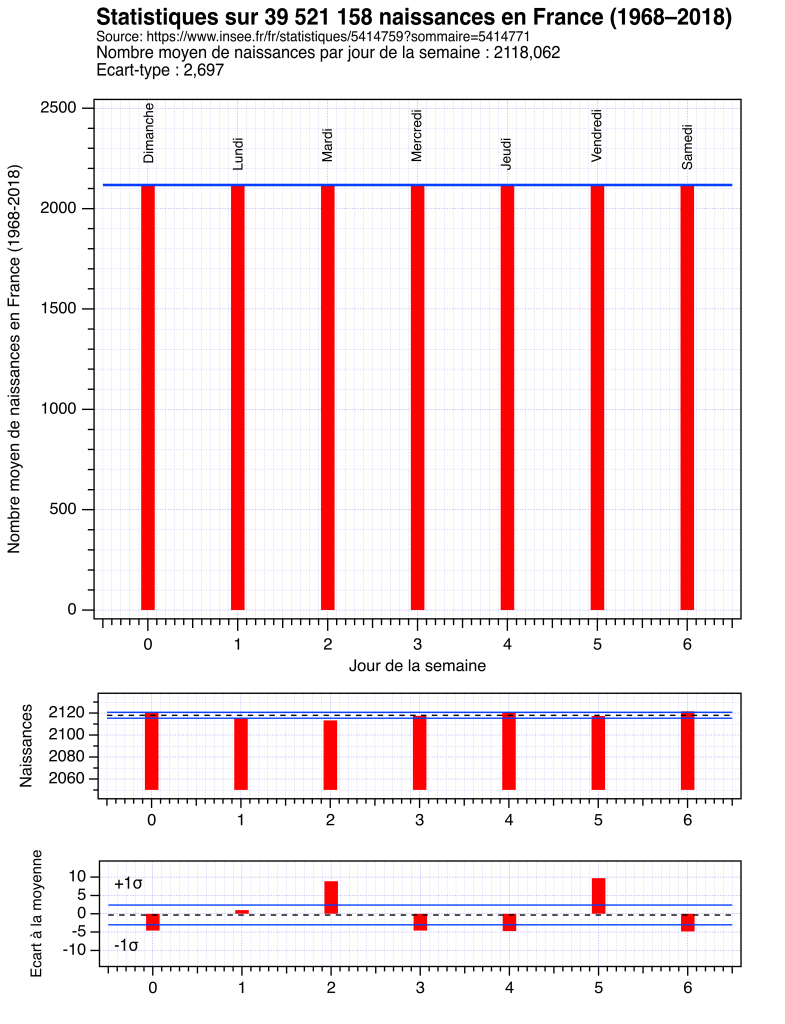
On peut de plus monter que la moyenne des naissances varie en réalité très peu selon le jour de la semaine.
Par contre, sur une année, il y a très clairement moins de naissances lors des jours fériés ! Cette fois-ci les écarts son bien significatifs, ainsi que le confirme la valeur p, très faible dans les cas très écartés de la moyenne.

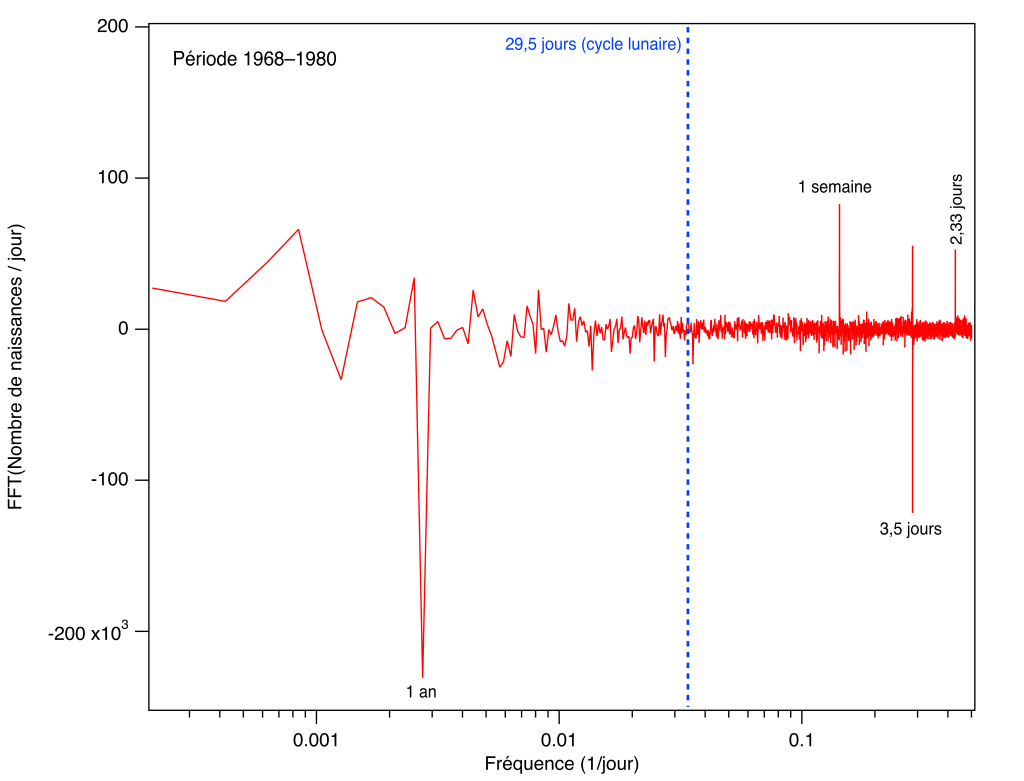
Enfin, une approche un peu plus mathématique : l’analyse de Fourier. Si nous prenons les données quotidiennes des naissances sur les 52 ans disponibles à l’INSEE et que l’on en effectue une Transformée de Fourier (techniquement ici, une FFT à l’aide du logiciel Igor Pro), on obtient les fréquences présentes dans ce « signal ». Ce qui est absolument remarquable, c’est qu’on trouve différentes périodes (qui s’expliquent plus ou moins), mais absolument pas celle correspondant au cycle lunaire.

La période annuelle correspond à la périodicité des jours fériés qui reviennent chaque année. Les périodicités de une semaine et moins correspondent à ce qui est observé plus haut sur le graphe des naissances selon le jour de la semaine. Il y a moins de naissances le dimanche, par exemple. C’est assez marginal, mais bien régulier, d’où la puissance de la transformée de Fourier pour sortir ces périodes. Quant à la périodicité de 73 jours (1/5 an), elle semble plus mystérieuse. Si on effectue la même opération en se limitant à la période 1968–1980, elle disparaît. Il semble qu’elle corresponde à la périodicité actuelle des vacances scolaires en France!
Complément :
Jean-Jacques Paul Andrieu a également écrit un article détaillé sur ce sujet, en utilisant une approche semblable mais des outils de calcul différents, sur son blog :
https://www.jjastrophotographie.fr/q4/?fbclid=IwAR1oC64DdSx4jI78Umh2riBXh8pifeqBqP73uhJ8ArtnSuFuTzug7q9jffM
